data_source
stringclasses 1
value | prompt
listlengths 1
1
| ability
stringclasses 1
value | reward_model
dict | extra_info
dict |
|---|---|---|---|---|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "A rectangle has length 8 cm and width $\\pi$ cm. A semi-circle has the same area as the rectangle. What is its radius?\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "4",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Given that $a_1, a_2, a_3, . . . , a_{99}$ is a permutation of $1, 2, 3, . . . , 99,$ find the maximum possible value of $$ |a_1 - 1| + |a_2 - 2| + |a_3 - 3| + \\dots + |a_{99} - 99|. $$\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "4900",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Consider the parabola consisting of the points $(x, y)$ in the real plane satisfying $(y+x)=(y-x)^{2}+3(y-x)+3$. Find the minimum possible value of $y$.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "-\\frac{1}{2}",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "In $\\triangle PQR,$ the sum of $\\angle P$ and $\\angle Q$ is $60^\\circ.$ What is the measure of $\\angle R?$\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "120^\\circ",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Given a power function $y = f(x)$ whose graph passes through the point $(4, 2)$, find $f\\left( \\frac{1}{2} \\right)$.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "\\frac{\\sqrt{2}}{2}",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Given that the wavelength of each light quantum is approximately $688$ nanometers and $1$ nanometer is equal to $0.000000001$ meters, express the wavelength of each light quantum in scientific notation.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "6.88\\times 10^{-7}",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Find the equation of the line that passes through the intersection of the lines $2x+3y+5=0$ and $2x+5y+7=0$, and is parallel to the line $x+3y=0$. Also, calculate the distance between these two parallel lines.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "\\frac{2\\sqrt{10}}{5}",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Qiang drives $15$ miles at an average speed of $30$ miles per hour. How many additional miles will he have to drive at $55$ miles per hour to average $50$ miles per hour for the entire trip?\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "110",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "If $x^2 + \\frac{1}{x^2} = A,$ and $x - \\frac{1}{x} = B,$ where $A$ and $B$ are positive numbers, find the minimum possible numerical value for $\\frac{A}{B}.$\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "2 \\sqrt{2}",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Calculate the surface integrals of the first kind:\na) \\(\\iint_{\\sigma}|x| dS\\), where \\(\\sigma\\) is defined by \\(x^2 + y^2 + z^2 = 1\\), \\(z \\geqslant 0\\).\n\nb) \\(\\iint_{\\sigma} (x^2 + y^2) dS\\), where \\(\\sigma\\) is defined by \\(x^2 + y^2 = 2z\\), \\(z = 1\\).\n\nc) \\(\\iint_{\\sigma} (x^2 + y^2 + z^2) dS\\), where \\(\\sigma\\) is the part of the cone defined by \\(z^2 - x^2 - y^2 = 0\\), \\(z \\geqslant 0\\), truncated by the cylinder \\(x^2 + y^2 - 2x = 0\\).\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "3\\sqrt{2} \\pi",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Given $\\frac{cos2α}{sin(α-\\frac{π}{4})}=-\\frac{\\sqrt{6}}{2}$, express $cos(α-\\frac{π}{4})$ in terms of radicals.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "\\frac{\\sqrt{6}}{4}",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Let $a \\clubsuit b = \\frac{2a}{b} \\cdot \\frac{b}{a}$. What is $(5 \\clubsuit (3 \\clubsuit 6)) \\clubsuit 1$?\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "2",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Given that Chelsea is ahead by 60 points halfway through a 120-shot archery contest, with each shot scoring 10, 8, 5, 3, or 0 points and Chelsea scoring at least 5 points on every shot, determine the smallest number of bullseyes (10 points) Chelsea needs to shoot in her next n attempts to ensure victory, assuming her opponent can score a maximum of 10 points on each remaining shot.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "49",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "In $\\triangle ABC$, the sides opposite to angles $A, B, C$ are denoted as $a, b, c$, respectively, and $a=1, A=\\frac{\\pi}{6}$.\n\n(Ⅰ) When $b=\\sqrt{3}$, find the magnitude of angle $C$; \n(Ⅱ) Find the maximum area of $\\triangle ABC$.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "\\frac{2+ \\sqrt{3}}{4}",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Given $-π < x < 0$, $\\sin x + \\cos x = \\frac{1}{5}$,\n(1) Find the value of $\\sin x - \\cos x$;\n(2) Find the value of $\\frac{3\\sin^2 \\frac{x}{2} - 2\\sin \\frac{x}{2}\\cos \\frac{x}{2} + \\cos^2 \\frac{x}{2}}{\\tan x + \\frac{1}{\\tan x}}$.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "-\\frac{132}{125}",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Evaluate $2000^3-1999\\cdot 2000^2-1999^2\\cdot 2000+1999^3$\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "3999",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "The circumcircle of acute $\\triangle ABC$ has center $O$ . The line passing through point $O$ perpendicular to $\\overline{OB}$ intersects lines $AB$ and $BC$ at $P$ and $Q$ , respectively. Also $AB=5$ , $BC=4$ , $BQ=4.5$ , and $BP=\\frac{m}{n}$ , where $m$ and $n$ are relatively prime positive integers. Find $m+n$ .\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "23",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Snow White has a row of 101 plaster dwarfs in her garden, arranged by weight from heaviest to lightest, with the weight difference between each pair of adjacent dwarfs being the same. Once, Snow White weighed the dwarfs and discovered that the first, heaviest dwarf weighs exactly $5 \\mathrm{~kg}$. Snow White was most surprised to find that when she put the 76th to 80th dwarf on the scale, they weighed the same as the 96th to 101st dwarf. What is the weight of the lightest dwarf?\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "2.5",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "The line $2x+ay-2=0$ is parallel to the line $ax+(a+4)y-4=0$. Find the value of $a$.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "-2",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "A modified octahedron consists of two pyramids, each with a pentagonal base, glued together along their pentagonal bases, forming a polyhedron with twelve faces. An ant starts at the top vertex and walks randomly to one of the five adjacent vertices in the middle ring. From this vertex, the ant walks again to another randomly chosen adjacent vertex among five possibilities. What is the probability that the second vertex the ant reaches is the bottom vertex of the polyhedron? Express your answer as a common fraction.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "\\frac{1}{5}",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "At a math competition, a team of $8$ students has $2$ hours to solve $30$ problems. If each problem needs to be solved by $2$ students, on average how many minutes can a student spend on a problem?\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "16",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Given the functions $f(x)=x^{2}+px+q$ and $g(x)=x+\\frac{1}{x^{2}}$ on the interval $[1,2]$, determine the maximum value of $f(x)$.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "4 - \\frac{5}{2} \\sqrt[3]{2} + \\sqrt[3]{4}",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Eight consecutive three-digit positive integers have the following property: each of them is divisible by its last digit. What is the sum of the digits of the smallest of these eight integers?\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "13",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Line $l$ in the coordinate plane has equation $3x-5y+40=0$. This line is rotated $45^{\\circ}$ counterclockwise about the point $(20,20)$ to obtain line $k$. What is the $x$-coordinate of the $x$-intercept of line $k?$\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "15",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Given the hyperbola $C$: $\\frac{x^2}{a^2} - \\frac{y^2}{b^2} = 1$ ($a > 0, b > 0$) with asymptotic equations $y = \\pm \\sqrt{3}x$, and $O$ as the origin, the point $M(\\sqrt{5}, \\sqrt{3})$ lies on the hyperbola.\n\n$(1)$ Find the equation of the hyperbola $C$.\n\n$(2)$ If a line $l$ intersects the hyperbola at points $P$ and $Q$, and $\\overrightarrow{OP} \\cdot \\overrightarrow{OQ} = 0$, find the minimum value of $|OP|^2 + |OQ|^2$.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "24",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Sector $OAB$ is a quarter of a circle with radius 5 cm. Inside this sector, a circle is inscribed, tangent at three points. Find the radius of the inscribed circle in simplest radical form.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "5\\sqrt{2} - 5",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "In a large bag of decorative ribbons, $\\frac{1}{4}$ are yellow, $\\frac{1}{3}$ are purple, $\\frac{1}{8}$ are orange, and the remaining 45 ribbons are silver. How many of the ribbons are orange?\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "19",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "The average yield per unit area of a rice variety for five consecutive years was 9.4, 9.7, 9.8, 10.3, and 10.8 (unit: t/hm²). Calculate the variance of this sample data.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "0.244",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Compute the number of positive four-digit multiples of 11 whose sum of digits (in base ten) is divisible by 11.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "72",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "The Aces are playing the Kings in a playoff series, where the first team to win 5 games wins the series. Each game's outcome leads to the Aces winning with a probability of $\\dfrac{7}{10}$, and there are no draws. Calculate the probability that the Aces win the series.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "90\\%",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Given non-zero vectors $\\overrightarrow{a}, \\overrightarrow{b}$, if $(\\overrightarrow{a} - 2\\overrightarrow{b}) \\perp \\overrightarrow{a}$ and $(\\overrightarrow{b} - 2\\overrightarrow{a}) \\perp \\overrightarrow{b}$, find the angle between $\\overrightarrow{a}$ and $\\overrightarrow{b}$.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "\\frac{\\pi}{3}",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "The area of the parallelogram generated by the vectors $\\mathbf{a}$ and $\\mathbf{b}$ is 8. Find the area of the parallelogram generated by the vectors $2 \\mathbf{a} + 3 \\mathbf{b}$ and $\\mathbf{a} - 5 \\mathbf{b}.$\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "104",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "On the last day of school, Mrs. Wonderful gave jelly beans to her class. She gave each boy as many jelly beans as there were boys in the class. She gave each girl as many jelly beans as there were girls in the class. She brought $400$ jelly beans, and when she finished, she had six jelly beans left. There were two more boys than girls in her class. How many students were in her class?\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "28",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Let $\\frac{x^2+y^2}{x^2-y^2} + \\frac{x^2-y^2}{x^2+y^2} = k$ . Compute the following expression in terms of $k$ : \\[E(x,y) = \\frac{x^8 + y^8}{x^8-y^8} - \\frac{ x^8-y^8}{x^8+y^8}.\\]\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "\\[\n\\boxed{\\frac{(k^2 - 4)^2}{4k(k^2 + 4)}}\n\\]",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "If $x, y, z \\in \\mathbb{R}$ are solutions to the system of equations $$ \\begin{cases}\nx - y + z - 1 = 0\nxy + 2z^2 - 6z + 1 = 0\n\\end{cases} $$ what is the greatest value of $(x - 1)^2 + (y + 1)^2$ ?\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "11",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Two distinct positive integers \\( x \\) and \\( y \\) are factors of 48. If \\( x \\cdot y \\) is not a factor of 48, what is the smallest possible value of \\( x \\cdot y \\)?\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "32",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Find $\\tan \\frac{9 \\pi}{4}.$\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "1",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "A 16-step path is to go from $(-4,-4)$ to $(4,4)$ with each step increasing either the $x$-coordinate or the $y$-coordinate by 1. How many such paths stay outside or on the boundary of the square $-2 < x < 2$, $-2 < y < 2$ at each step?\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "1698",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "The equation of the line that passes through the points $(-2,0)$ and $(0,2)$ can be expressed in the form $y=mx+b$. What is the value of $m+b$?\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "3",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "A whole number, $M$, is chosen so that $\\frac{M}{4}$ is strictly between 8 and 9. What is the value of $M$?\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "33",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Let $x = 2001^{1002} - 2001^{-1002}$ and $y = 2001^{1002} + 2001^{-1002}.$ Find $x^2 - y^2.$\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "-4",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "For all $n \\geq 1$, let \\[ a_n = \\sum_{k=1}^{n-1} \\frac{\\sin \\left( \\frac{(2k-1)\\pi}{2n} \\right)}{\\cos^2 \\left( \\frac{(k-1)\\pi}{2n} \\right) \\cos^2 \\left( \\frac{k\\pi}{2n} \\right)}. \\] Determine \\[ \\lim_{n \\to \\infty} \\frac{a_n}{n^3}. \\]\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "\\frac{8}{\\pi^3}",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Given that five boys, A, B, C, D, and E, are randomly assigned to stay in 3 standard rooms (with at most two people per room), calculate the probability that A and B stay in the same standard room.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "\\frac{1}{5}",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "How many integers between 100 and 300 are multiples of both 5 and 7, but are not multiples of 10?\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "3",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "If Jeff picks one letter randomly from the alphabet, what is the probability that the letter is in the word `PROBABILITY'?\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "\\frac{9}{26}",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Consider a $4 \\times 4$ grid of squares with 25 grid points. Determine the number of different lines passing through at least 3 of these grid points.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "32",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Anya wants to buy ice cream that costs 19 rubles. She has two 10-ruble coins, two 5-ruble coins, and one 2-ruble coin in her pocket. Anya randomly picks three coins from her pocket without looking. Find the probability that the selected coins will be enough to pay for the ice cream.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "0.4",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "A farmer buys 600 cows. He sells 500 of them for the price he paid for all 600 cows. The remaining 100 cows are sold for 10% more per cow than the price of the 500 cows. Calculate the percentage gain on the entire transaction.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "22\\%",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "If $$log_{4}(a+4b)=log_{2}2 \\sqrt {ab}$$, find the minimum value of $a+b$.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "\\frac{9}{4}",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Employees from department X are 30, while the employees from department Y are 20. Since employees from the same department do not interact, the number of employees from department X that will shake hands with the employees from department Y equals 30, and the number of employees from department Y that will shake hands with the employees from department X also equals 20. Find the total number of handshakes that occur between employees of different departments.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "600",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "What describes the set of values of $a$ for which the curves $x^2+y^2=a^2$ and $y=x^2-a$ in the real $xy$-plane intersect at exactly 3 points?\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "a>\\frac{1}{2}",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "In a company, some pairs of people are friends (if $A$ is friends with $B$, then $B$ is friends with $A$). It turns out that among every set of 100 people in the company, the number of pairs of friends is odd. Find the largest possible number of people in such a company.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "101",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Simplify first, then evaluate: $4(3a^{2}b-ab^{2})-(2ab^{2}+3a^{2}b)$, where $a=\\frac{1}{3}$ and $b=-1$.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "-3",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Find the sum of the digits in the number $\\underbrace{44 \\ldots 4}_{2012 \\text{ times}} \\cdot \\underbrace{99 \\ldots 9}_{2012 \\text{ times}}$.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "18108",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Twelve tiles numbered $1$ through $12$ are turned up at random, and an eight-sided die is rolled. Calculate the probability that the product of the numbers on the tile and the die will be a perfect square.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "\\frac{13}{96}",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "In the rectangular coordinate system $(xOy)$, if the initial side of angle $\\alpha$ is the non-negative semi-axis of $x$, and the terminal side is the ray $l$: $y=2x(x\\leqslant 0)$.\n\n(1) Find the value of $\\tan \\alpha$;\n\n(2) Find the value of $\\frac{\\cos \\left(\\alpha-\\pi\\right)-2\\cos \\left( \\frac{\\pi}{2}+\\alpha\\right)}{\\sin \\left(\\alpha- \\frac{3\\pi}{2}\\right)-\\sin \\alpha}$.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "-3",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "A stalker, to detect a gravitational anomaly (an area where the acceleration due to gravity changes sharply in magnitude), throws a small nut from the surface of the Earth at an angle \\(\\alpha = 30^\\circ\\) to the horizontal with a speed \\(v_0 = 20 \\, \\text{m/s}\\). The normal acceleration due to gravity is \\(g = 10 \\, \\text{m/s}^2\\). At the highest point of its trajectory, the nut enters the anomaly zone and continues to move in it. As a result, the nut falls to the Earth at a distance of \\(S = 15\\sqrt{3}\\) meters from the stalker. Determine the acceleration due to gravity inside the anomaly. (15 points)\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "40",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "In the decimal representation of an even number \\( M \\), only the digits \\( 0, 2, 4, 5, 7, \\) and \\( 9 \\) are used, and the digits may repeat. It is known that the sum of the digits of the number \\( 2M \\) equals 39, and the sum of the digits of the number \\( M / 2 \\) equals 30. What values can the sum of the digits of the number \\( M \\) take? List all possible answers.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "33",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Suppose $A B C$ is a triangle with circumcenter $O$ and orthocenter $H$ such that $A, B, C, O$, and $H$ are all on distinct points with integer coordinates. What is the second smallest possible value of the circumradius of $A B C$ ?\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "\\sqrt{10}",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "A solid box is 20 cm by 15 cm by 12 cm. A new solid is formed by removing a cube 4 cm on a side from each of the top four corners of this box. After that, four cubes, 2 cm on a side, are placed on each lower corner of the box. What percent of the original volume has been altered (either lost or gained)?\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "6.22\\%",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "An eight-sided die numbered from 1 to 8 is rolled, and $P$ is the product of the seven numbers that are visible. What is the largest number that is certain to divide $P$?\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "48",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "How many ways are there to arrange numbers from 1 to 8 in circle in such way the adjacent numbers are coprime?\n\nNote that we consider the case of rotation and turn over as distinct way.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "72",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "The fenced area of a yard is a 15-foot by 12-foot rectangular region with a 3-foot by 3-foot square cut out, as shown. What is the area of the region within the fence, in square feet?\n\n[asy]draw((0,0)--(16,0)--(16,12)--(28,12)--(28,0)--(60,0)--(60,48)--(0,48)--cycle);\nlabel(\"15'\",(30,48),N);\nlabel(\"12'\",(60,24),E);\nlabel(\"3'\",(16,6),W);\nlabel(\"3'\",(22,12),N);\n[/asy]\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "171",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Given $A=\\{4, a^2\\}$, $B=\\{a-6, a+1, 9\\}$, if $A \\cap B = \\{9\\}$, find the value of $a$.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "-3",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Masha has three identical dice, each face of which has one of six different prime numbers with a total sum of 87.\n\nMasha rolled all three dice twice. The first time, the sum of the numbers rolled was 10, and the second time, the sum of the numbers rolled was 62.\n\nExactly one of the six numbers never appeared. What number is it?\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "17",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "What is the area of the smallest square that can completely contain a circle with a radius of 5?\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "100",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "A light flashes in one of three different colors: red, green, and blue. Every $3$ seconds, it flashes green. Every $5$ seconds, it flashes red. Every $7$ seconds, it flashes blue. If it is supposed to flash in two colors at once, it flashes the more infrequent color. How many times has the light flashed green after $671$ seconds?\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "154",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Out of the digits 0 through 9, three digits are randomly chosen to form a three-digit number without repeating any digits. What is the probability that this number is not divisible by 3?\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "2/3",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Amy, Beth, and Claire each have some sweets. Amy gives one third of her sweets to Beth. Beth gives one third of all the sweets she now has to Claire. Then Claire gives one third of all the sweets she now has to Amy. All the girls end up having the same number of sweets.\n\nClaire begins with 40 sweets. How many sweets does Beth have originally?\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "50",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Suppose the graph of $y=f(x)$ includes the points $(1,5),$ $(2,3),$ and $(3,1)$.\n\nBased only on this information, there are two points that must be on the graph of $y=f(f(x))$. If we call those points $(a,b)$ and $(c,d),$ what is $ab+cd$?\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "17",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Find the common ratio of the infinite geometric series: $$\\frac{5}{6}-\\frac{4}{9}+\\frac{32}{135}-\\dots$$\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "-\\frac{8}{15}",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Find the maximum value of the function\n$$\nf(x) = \\sqrt{3} \\sin 2x + 2 \\sin x + 4 \\sqrt{3} \\cos x.\n$$\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "\\frac{17}{2}",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "For the cubic function $f(x)=ax^3+bx^2+cx+d$ ($a\\neq 0$), define: Let $f''(x)$ be the derivative of the derivative of the function $y=f(x)$, that is, the second derivative of $f(x)$. If the equation $f''(x)=0$ has a real solution $x_0$, then the point $(x_0, f(x_0))$ is called the \"inflection point\" of the function $y=f(x)$. Some students found that \"every cubic function has an 'inflection point'; every cubic function has a center of symmetry; and the 'inflection point' is the center of symmetry.\" Based on this discovery, for the function $$f(x)=x^3- \\frac{3}{2}x^2+3x- \\frac{1}{4},$$ its center of symmetry is ___________; calculate $$f\\left( \\frac{1}{2013}\\right)+f\\left( \\frac{2}{2013}\\right)+f\\left( \\frac{3}{2013}\\right)+\\cdots +f\\left( \\frac{2012}{2013}\\right)$$ = ___________.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "2012",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "If $a$ and $b$ are integers such that $x^2 - x - 1$ is a factor of $ax^3 + bx^2 + 1,$ find $b.$\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "-2",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "The residents of an accommodation need to pay the rent for the accommodation. If each of them contributes $10 \\mathrm{Ft}$, the amount collected falls $88 \\mathrm{Ft}$ short of the rent. However, if each of them contributes $10.80 \\mathrm{Ft}$, then the total amount collected exceeds the rent by $2.5 \\%$. How much should each resident contribute to collect exactly the required rent?\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "10.54",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Determine how many integers are in the list containing the smallest positive multiple of 30 that is a perfect square, the smallest positive multiple of 30 that is a perfect cube, and all the multiples of 30 between them.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "871",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "In $\\triangle ABC$, the lengths of the sides opposite to angles $A$, $B$, and $C$ are $a$, $b$, and $c$ respectively, with $c=2$ and $C=\\frac{\\pi}{3}$.\n1. If the area of $\\triangle ABC$ is $\\sqrt{3}$, find $a$ and $b$.\n2. If $\\sin B = 2\\sin A$, find the area of $\\triangle ABC$.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "\\frac{4\\sqrt{3}}{3}",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "The value of $3x + 15$ is one third of the value of $6x + 45$. After finding $x$, subtract 5 from the result. What is the final value?\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "-5",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "In a two-day problem-solving tournament, Alpha and Gamma both attempted questions worth a total of 600 points. Alpha scored 210 points out of 350 points on the first day, and 150 points out of 250 points on the second day. Gamma, who did not attempt 350 points on the first day, had a positive integer score on each of the two days, and Gamma's daily success ratio (points scored divided by points attempted) on each day was less than Alpha's on that day. Alpha's two-day success ratio was $\\frac{360}{600} = 3/5$.\n\nFind the largest possible two-day success ratio that Gamma could have achieved.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "\\frac{359}{600}",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Say that an integer $A$ is yummy if there exist several consecutive non-negative integers, including $A$, that add up to 2023. What is the smallest yummy integer?\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "1011",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Given $sinα-cosα=\\frac{1}{5},0≤α≤π$, calculate $sin(2α-\\frac{π}{4})$.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "\\frac{31\\sqrt{2}}{50}",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Given that the terminal side of angle $\\varphi$ passes through point P(1, -1), and points A($x_1$, $y_1$) and B($x_2$, $y_2$) are any two points on the graph of the function $f(x) = \\sin(\\omega x + \\varphi)$ ($\\omega > 0$). If $|f(x_1) - f(x_2)| = 2$, the minimum value of $|x_1 - x_2|$ is $\\frac{\\pi}{3}$. Find the value of $f\\left(\\frac{\\pi}{2}\\right)$.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "-\\frac{\\sqrt{2}}{2}",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "The sides of a triangle have lengths $13, 17,$ and $m,$ where $m$ is a positive integer. For how many values of $m$ is the triangle obtuse?\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "14",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "The value of the expression \\(10 - 10.5 \\div [5.2 \\times 14.6 - (9.2 \\times 5.2 + 5.4 \\times 3.7 - 4.6 \\times 1.5)]\\) is\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "9.3",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Suppose $a$ and $b$ are positive integers. Isabella and Vidur both fill up an $a \\times b$ table. Isabella fills it up with numbers $1,2, \\ldots, a b$, putting the numbers $1,2, \\ldots, b$ in the first row, $b+1, b+2, \\ldots, 2 b$ in the second row, and so on. Vidur fills it up like a multiplication table, putting $i j$ in the cell in row $i$ and column $j$. Isabella sums up the numbers in her grid, and Vidur sums up the numbers in his grid; the difference between these two quantities is 1200. Compute $a+b$.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "21",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "The value of $y$ varies inversely as $\\sqrt x$ and when $x=2$, $y=4$. What is $x$ when $y=1$?\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "32",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Grandma gave Bryce and Carter some raisins. Bryce received 6 more raisins than Carter, and Carter received half the number of raisins Bryce received. How many raisins did Bryce receive?\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "12",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Given that $[x]$ represents the greatest integer less than or equal to $x$, if\n$$\n[x+0.1]+[x+0.2]+[x+0.3]+[x+0.4]+[x+0.5]+[x+0.6]+[x+0.7]+[x+0.8]+[x+0.9]=104\n$$\n\nthen the smallest value of $x$ is ( ).\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "11.5",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "The numbers from 1 to 9 are placed in the cells of a $3 \\times 3$ table such that the sum of the numbers on one diagonal is 7, and on the other diagonal is 21. What is the sum of the numbers in the five shaded cells?\n\n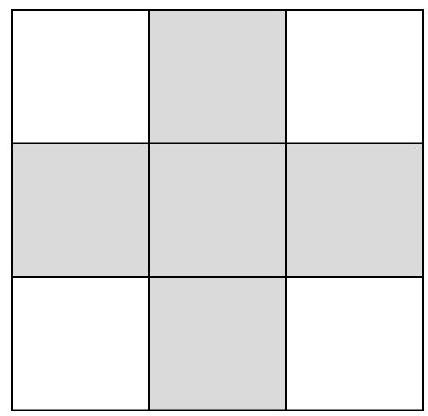\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "25",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Let $n$ be a 5-digit number, and let $q$ and $r$ be the quotient and the remainder, respectively, when $n$ is divided by 50. Determine the number of values of $n$ for which $q+r$ is divisible by 7.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "12600",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Calculate the value of $V_3$ in Horner's method (also known as Qin Jiushao algorithm) for finding the value of the polynomial $f(x) = 4x^6 + 3x^5 + 4x^4 + 2x^3 + 5x^2 - 7x + 9$ when $x = 4$.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "80",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "In the diagram, if the area of $\\triangle ABC$ is 36 where $A(3, 15)$, $B(15, 0)$, and $C(0, q)$ lie on a Cartesian plane. Determine the value of $q$.\n[asy]\nsize(5cm);defaultpen(fontsize(9));\npair a = (3, 15); pair b = (15, 0); pair c = (0, 12);pair d= (3, 0);\ndraw(a--b--c--cycle);\n\nlabel(\"$A(3, 15)$\", a, N);\nlabel(\"$B(15, 0)$\", b, S);\nlabel(\"$C(0, q)$\", c, W);\nlabel(\"$x$\", (17, 0), E);\nlabel(\"$y$\", (0, 17), N);\ndraw((-2,0)--(17,0), Arrow);\ndraw((0,-2)--(0,17), Arrow);\n[/asy]\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "12.75",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Given that the sequence {a<sub>n</sub>} is an arithmetic sequence, if $\\frac {a_{11}}{a_{10}}$ < -1, and its first n terms sum S<sub>n</sub> has a maximum value, determine the maximum value of n that makes S<sub>n</sub> > 0.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "19",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Given the polar equation of a circle is $\\rho=2\\cos \\theta$, the distance from the center of the circle to the line $\\rho\\sin \\theta+2\\rho\\cos \\theta=1$ is ______.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "\\dfrac { \\sqrt {5}}{5}",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Given a square $ABCD$ . Let $P\\in{AB},\\ Q\\in{BC},\\ R\\in{CD}\\ S\\in{DA}$ and $PR\\Vert BC,\\ SQ\\Vert AB$ and let $Z=PR\\cap SQ$ . If $BP=7,\\ BQ=6,\\ DZ=5$ , then find the side length of the square.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "10",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "A four-digit natural number $M$, where the digits in each place are not $0$, we take its hundreds digit as the tens digit and the tens digit as the units digit to form a new two-digit number. If this two-digit number is greater than the sum of the thousands digit and units digit of $M$, then we call this number $M$ a \"heart's desire number\"; if this two-digit number can also be divided by the sum of the thousands digit and units digit of $M$, then we call this number $M$ not only a \"heart's desire\" but also a \"desire fulfilled\". [\"Heart's desire, desire fulfilled\" comes from \"Analects of Confucius. On Governance\", meaning that what is desired in the heart becomes wishes, and all wishes can be fulfilled.] For example, $M=3456$, since $45 \\gt 3+6$, and $45\\div \\left(3+6\\right)=5$, $3456$ is not only a \"heart's desire\" but also a \"desire fulfilled\". Now there is a four-digit natural number $M=1000a+100b+10c+d$, where $1\\leqslant a\\leqslant 9$, $1\\leqslant b\\leqslant 9$, $1\\leqslant c\\leqslant 9$, $1\\leqslant d\\leqslant 9$, $a$, $b$, $c$, $d$ are all integers, and $c \\gt d$. If $M$ is not only a \"heart's desire\" but also a \"desire fulfilled\", where $\\frac{{10b+c}}{{a+d}}=11$, let $F\\left(M\\right)=10\\left(a+b\\right)+3c$. If $F\\left(M\\right)$ can be divided by $7$, then the maximum value of the natural number $M$ that meets the conditions is ____.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "5883",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Kevin has an elm tree in his yard that is $11\\frac{2}{3}$ feet tall and an oak tree that is $17\\frac{5}{6}$ feet tall. How much taller is the oak tree than the elm tree? Express your answer as a simplified mixed number.\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "6\\frac{1}{6}\\text{ feet}",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Let $f$ be a random permutation on $\\{1, 2, \\dots, 100\\}$ satisfying $f(1) > f(4)$ and $f(9)>f(16)$ . The probability that $f(1)>f(16)>f(25)$ can be written as $\\frac mn$ where $m$ and $n$ are relatively prime positive integers. Compute $100m+n$ .\n\nNote: In other words, $f$ is a function such that $\\{f(1), f(2), \\ldots, f(100)\\}$ is a permutation of $\\{1,2, \\ldots, 100\\}$ .\n\n*Proposed by Evan Chen*\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "124",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "Cirlce $\\Omega$ is inscribed in triangle $ABC$ with $\\angle BAC=40$ . Point $D$ is inside the angle $BAC$ and is the intersection of exterior bisectors of angles $B$ and $C$ with the common side $BC$ . Tangent form $D$ touches $\\Omega$ in $E$ . FInd $\\angle BEC$ .\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "110",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
DigitalLearningGmbH/MATH-lighteval
|
[
{
"content": "The value of \\((4 + 44 + 444) \\div 4\\) is:\nPlease reason step by step, and put your final answer within \\boxed{}.",
"role": "user"
}
] |
math
|
{
"ground_truth": "123",
"style": "rule-lighteval/MATH_v2"
}
|
{
"dataset": "deepscaler"
}
|
End of preview. Expand
in Data Studio
README.md exists but content is empty.
- Downloads last month
- 5